History of Maxwell’s Equations: #1 Gauss’s Law

I would like to start with a little story. In the late 1950s the faculty of Caltech became concerned that the physics undergraduate curriculum was out of date and wasn’t keeping up with the exciting new developments in Physics, including the discoveries developed by one of their star professors named Richard Feynman.

So, as Feynman was an excellent teacher and a frequent vocal complainer about this very issue, they asked him to teach a new revamped 2-year undergraduate class on basic physics.

He agreed, but only for one time, which is why every lecture was recorded and every drawing photographed.

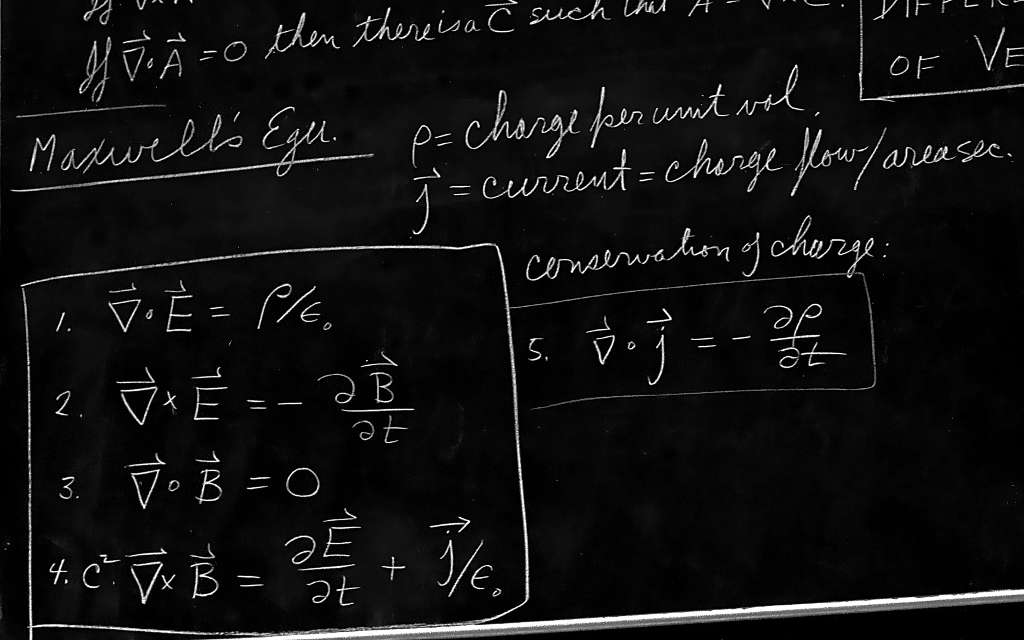
These series of lectures were so beloved that they were immediately made into a book “The Feynman Lectures in Physics” which are considered the gold standard of Physics where they continue to inspire and influence physics education to this day.^[1]

The reason I mention Feynman and the Feynman lectures is that, like many theoretical physicists, Feynman was deeply enamored of Maxwell’s laws.  In fact, Feynman started his lecture by stating that, “There can be little doubt that the most significant event of the 19^th century will be judged as Maxwell’s discovery of the laws of electrodynamics. The American Civil War will pale into provincial insignificance in comparison.”^[2] Whew. Feynman also concluded with the statement that “Maxwell… brought together all of the laws of electricity and magnetism and made one complete and beautiful theory.”^[3]

However, despite Feynman’s well-deserved reputation for the excellence in his lectures, particularly his ones about electricity and magnetism, Feynman admitted that something was missing. I will let him tell it. Roll the tape.^[4]

So, I thought, I have the time – why don’t I take a crack at it?

Thus, with a mix of hubris and an obsession with history, I have decided to talk about the historical development of the 4 modern forms of Maxwell’s equations in a series of videos.

This is my first video, on the history of physics experiments and theories behind Gauss’ Law.

This is a story that starts with Charles Augustin Coulomb and how he inspired Michael Faraday, then how Faraday inspired James Clerk Maxwell and why Maxwell’s equations as he wrote them are equivalent to our modern version of his “Gauss’s equation” law, albeit with different letters, names, and math conventions. Ready? Let’s Go!

---

---

Table of Contents

Part 1: Coulomb’s Law and Experiments (1784-1786)

Part 2: Faraday’s Electric Lines & Dielectrics (1837)

Part 3: Maxwell “On Faraday’s Lines of Force” (1855-56)

Part 4: Maxwell’s “On Physical Lines of Force” (1861-62) 

Part 5: Maxwell’s “Electric Elasticity” vs. Heaviside’s “Permittivity”

References

---

Part 1: Coulomb’s Law and Experiments (1784-1786)

I would like to start sometime in the early 1780s when a French engineer named Charles Augustin Coulomb was told that there was a problem with his sensitive magnetic compass. 

It turns out that the compass was too sensitive as it would move whenever an operator would walk to the machine to take measurements. After viewing it himself, Coulomb realized that the machine was just reacting to the static charge acquired by the shuffling assistant.^[5]

They gave the assistant a grounding wire (and possibly removed a carpet) which solved the problem but it got Coulomb thinking, maybe a twisting machine could make a very sensitive scale, so sensitive it could measure the minute electrical forces.

Inspired, Coulomb studied the physics of twisting and, in 1784, presented a paper on what is called a torsional balance (or twisting scale), which was the world’s most precise measuring device at the time. A degree on the scale was equivalent to 1/100,000^th of the weight of a single grain of sand!^[6]

By 1785, Coulomb used that scale to study electric repulsion. He did this by charging up a tube by rubbing and then having it touch a ball in the scale. He then moved an identical metal ball until they touched, and then studied the repelling forces. In this way Coulomb experimentally determined that electrical repulsion force is proportional to one over the distance squared which he confidently wrote was a “Fundamental law of Electricity.”^[7] 

For his second paper on electricity, Coulomb studied attractive forces by charging one object by rubbing a glass tube and touching one sphere, while the second sphere was electrified by being touched by a wax or resin tube that was rubbed. In this way, Coulomb determined that the attractive force of opposite charges follows the same relationship.

In addition, Coulomb determined that the electric force depends linearly on the changes. Of course, he couldn’t directly measure the amount of charge (which is currently measured in Coulombs). 

Instead, he touched a charged ball in the balance with a neutral ball of the same size and then removed the outside ball to reduce the charge on the ball in the balance by 2, and found that the force would then also be reduced by 2.^[8]

After a third paper on how electricity dissipates over time, for his fourth paper, which was published the following year in 1786, Coulomb decided to use his electrometer to study how charges are distributed in conducting spheres. Coulomb then found, “That for conductive objects the electric fluid is only diffused over its surface, and does not penetrate into its interior parts.”^[9] 

Fast forward 50 years to 1836 a 45-year-old Michael Faraday read an English translation of Coulomb’s work and was fascinated. In fact, Coulomb’s fourth paper with the material about how charges reside on a conductor in particular directly influenced Michael Faraday to discover electric lines and dielectrics which brings us to..

Part 2: Faraday’s Electric Lines & Dielectrics (1837)

When Faraday read Coulomb’s papers it was 5 years after Faraday had discovered magneto-electric induction (or changing a magnetic field in a coil of wire could induce a current in that wire) and Faraday was on a tear of innovation about electricity.

That is why the next year, 1837, for his 11^th major Electricity paper in 6 years, Faraday then repeated Coulomb’s experiments with detecting charge on metal surfaces.

Then, Faraday upscaled Coulomb’s experiments and built a giant cube that he “lived in” while electrical experiments were conducted outside and found he was shielded from these forces.^[10]

Faraday immediately realized that what was going on was due to static electric induction – or charged objects moving charges without touching. As he wrote, “the effects are clearly inductive effects produced by electricity.”^[11] Because of this experiment Faraday imagined that all charged objects emanated what he called “lines of inductive force”^[12] or as he later called it “lines of electric force.”^[13]

What Faraday imagined was that all charged particles emit lines of force, and if you have multiple charges then all the lines from the opposite charges cancel out and the total surplus of charges emit a force field depending on the amount of extra charge. This force field will cause a force on any other charge you put in that field where the amount of force depends on the amount of charge you add times the strength of the electric field (F=qE).

As everything you can see is composed of an unfathomable amount of positive and negative charges, Electric fields have an effect on all visible matter. (Note: Electric fields do not affect Neutrons, but Faraday didn’t know about that as the Neutron wasn’t even theorized for a further 73 years).

I have a whole video (and script) about The Physics of the Faraday Cage.

Anyway, if the material is a conductor, the charges move until the Electric field inside the conductor is zero. This is why if you are surrounded by a metal cage called a Faraday cage, you are protected from the Electric field but if you pop your head out of the cage, the Electric field can make a visible effect.

If the material is an insulator, Faraday theorized that the molecules polarized but did not fully move to cancel out the field. For this reason, he came up with a new term for insulators, he called them: “dielectrics, to express that substance through which the electric forces are acting.”^[14]

The next immediate question is, do different materials affect the electric field more than others? Or as he put it: “I now proceed to examine the great question of specific inductive capacity ie. whether different dielectric bodies actually do possess any influence over the degree of induction which takes place through them.”^[15]

At the time they had known that two conductors separated by an insulator could store charge in something that they called a Leyden jar but which is now called a capacitor or condenser.

Therefore, Faraday examined how differently shaped “Leyden jars” worked when you inserted a dielectric and found that it would increase the charge on the capacitor. He then took a few samples in this way and found for example, that the specific inductive capacity (dielectric constant) of shellac is about 2 or twice that of air.^[16]

To recap, in late 1837, Faraday built the Faraday cage, created the *idea* of electric field lines (which he first called “inductive lines of force” and then “electric lines of force”), theorized that conductors let charges move to delete the “electric lines of force” within them to explain the Faraday cage, coined the name dielectrics to describe inductors as they can twist due to these lines of force, created the idea that different dielectrics have different electrical effects and a method to measure the dielectric constant that he just devised! Whew!

Faraday was very excited about his new ideas, and two months later in January, 1838 published another paper with the subtitle: “on induction (continued)”, in February, another “on induction (continued)” and in June, 1838 a paper of the “Nature of the Electric Force,” which was all about lines of induction.^[17]

Although Faraday was convinced that curved “inductive lines of force” or “electric lines of force” explained everything, most other scientists HATED it. It seems that the problem that most people had was with *curved* lines of force as everyone knew that forces moved in straight lines. Also, Faraday’s work had almost no mathematics, as Faraday had no math skills, which was displeasing to many physicists.

Then, Faraday had another problem. On November 29, 1839, Queen Victoria’s personal physician, Dr. Peter Latham, made an emergency visit as Faraday was so dizzy that he could barely walk and was having horrible memory issues. Dr. Latham wrote that Faraday said, “that his mind for a long time been dreadfully overworked” from not only “his own abstruse speculations upon electricity” but also all of his lectures and constant consultations.^[18]

Faraday tried to keep on teaching but the doctor said that if he didn’t take at least a year off, “he will suddenly break down,” and Faraday reluctantly stepped away from science.^[19] Faraday then spent years away from the laboratory and struggled with even reading other scientific texts, although whenever he had a moment of scientific lucidity he would be back in the laboratory where he still managed to make astonishing discoveries.

For example, he found a relationship between the polarization of light and magnets in 1845^[20] and proposed that light (radiation) was a wave of electric and/or magnetic lines of force in 1846.^[21] (I will go into all of this much more in further videos, don’t worry).

Then on February 20, 1853, almost 16 years after Faraday proposed the crazy idea of electric lines of force and dielectrics and 6 years after Faraday proposed the even crazier idea that light was a wave in these lines of force a 22-year-old Scottish mathematician and physicist named James Clerk Maxwell wrote his mentor, William Thomson (aka. Lord Kelvin) a letter.

Maxwell told Thomson that, “several of us here wish to attack Electricity” and asked if he should start with Faraday (who has no mathematics) or Ampère (who had quite a lot).^[22] Thomson recommended Faraday and, as Maxwell recalled, “as I proceeded with the study of Faraday, I perceived that his method of conceiving the phenomena was also a mathematical one, though not exhibited in the conventional form of mathematical symbols.” Moreover, Maxwell, who was very comfortable with mathematics, felt that he had the ability to convert Faraday’s “math” into “the ordinary mathematical forms.”^[23] Which brings us to…

Part 3: Maxwell “On Faraday’s Lines of Force” (1855-56)

In December of 1855, when Maxwell was just 24-years-old, he gave a talk titled “On Faraday’s Lines of Force.” According to Maxwell’s introduction, he wasn’t “attempting to establish any physical theory of a science in which I have hardly made a single experiment.” Instead, Maxwell wanted, “to show how, by a strict application of the ideas and methods of Faraday, the connection of the very different orders of phenomena which he has discovered may be clearly placed before the mathematical mind.”^[24]

In this paper, Maxwell had a challenge as Faraday not only had conceived of “lines of force” emanating from and to charged particles but, as a biographer of Maxwell’s put it, “Faraday went further than this; he conceived the notion of causing the lines of force to represent also the intensity of the force at every point, so that when the force is great the lines might be close together, and far apart when the force is small.”^[25]

Maxwell thus had to find a way to model not only, “the direction of the force, but [also] some method of indicating the intensity of the force at any point.” Maxwell’s initial solution was to model these lines of force, “not as mere lines, but as fine tubes of variable section carrying an incompressible fluid.”

His logic in this was he could use the physics of fluid dynamics to model how the electric force varying as one over the distance squared by changing the width of the tube, “since the velocity of the fluid is inversely as the section of the tube.”^[26](Note that Maxwell wasn’t thinking that these tubes were real, but using what he called a “purely imaginary substance” as a metaphor).^[27]

Maxwell then imagined that the positive charges were “sources” of these tubes and the negative charges were “sinks” of these tubes where the electrical lines of force flowed in the tubes continually.^[28]

Maxwell began with determining how the “pressure” of the “fluid” in the tubes changed with distance from the sources and sinks. He then declared that for any arrangement of these sources and sinks, there must be a surface with equal pressure, as the “pressure” is high near the sources and zero infinitely far away and it continuously changes. He then declared that, “it is easy to see that these surfaces of equal pressure must be perpendicular to the lines of fluid motion.”^[29]

If this sounds suspiciously like Maxwell was saying that charged particles have surfaces of equal potential and that the Electric field is dependent on the change in the potential over space, or what is called the gradient of the field, well, then you are 100% correct. And the astonishing thing is, Maxwell knew it! He outright stated that this “pressure” was the same as the voltage from a battery (then called the “electric tension”) and even more impressively, Maxwell connected this “electric tension” to the “potential in static electricity” writing: “This pressure, which is commonly called electric tension is found to be physically identical with the potential in static electricity, and thus we have the means of connecting the two sets of phenomena.”^[30]

Maxwell even went as far as deriving the “pressure” due to a source S in a uniform medium and got p=\frac{k}{4\pi} \frac{S}{r} which is exactly the same as the modern definition of potential from a point charge V=k\frac{Q}{r} I know it looks a bit different but that is only because Maxwell’s constant k is 4\pi times larger than modern “Coulomb’s constant” k (it seems likely that Coulomb’s constant is given the letter k because of Maxwell).^[31]

Also, note that Maxwell was frustrated with the added 4\pi in the “pressure” equation and over the years he would play with adding and removing 4\pi all over the place as you either have 4\pi in Gauss’s equation or in your equations for electric potential and field from a point charge (or use two constants).

Then, in his second talk on “Faraday’s lines of Force” which was given in February of 1856, he continued the analogy of a flow in pipes and connected the “electromotive force” or the “intensity of the electric action” (ie. the Electric field) to what he called the “quantity of electrical current” times a “resistance” k.

Note that Maxwell didn’t have vector multiplication, so he wrote three equations for the three directions, which he labeled equation [B]. But if we define the “intensity of the electric action” as the vector \overrightarrow{E}, and the “quantity of electric current” as the vector \overrightarrow{D}, then equation [B] is simply \overrightarrow{E} = k \overrightarrow{D}.

Note that this “quantity of electrical current” is actually the quantity of electrical lines emanating from or to a charge source or sink. As I feel this is confusing, I am going to give this variable the temporary name of “quantity of electric lines,” just so you don’t think I am talking about an actual current.

Anyway, Maxwell needed a way to determine how these “quantity of electric lines” were changing as they emerged from a source or entered a sink. That is why Maxwell used a math method that he gained from the great German mathematician, Carl Friedrich Gauss, where he imagined a surface in space and stated that the “total quantity of conduction through any surface” depends on how much of these lines, \overrightarrow{D} point out of the surface.

Maxwell then used calculus to show that if you integrated how much of the \overrightarrow{D} pointed out of the surface s, it was equivalent to the integral of the derivative of each component of the vector over the total volume in that surface.

Or, in modern math, he demonstrated that:

\oint \overrightarrow{D} \cdot d\overrightarrow{S} = \int\int\int \bigg(\frac{dD_x}{dx}+\frac{dD_y}{dy}+\frac{dD_z}{dz} \bigg)dxdydz

Note that the sum of derivatives \bigg(\frac{dD_x}{dx}+\frac{dD_y}{dy}+\frac{dD_z}{dz} \bigg) is now called the divergence of \overrightarrow{D} and can be written as \overrightarrow{\nabla}\cdot\overrightarrow{D}.

Then Maxwell made one of the most astonishing statements in Physics, he just said, basically, “hey let’s make all those derivatives (\overrightarrow{\nabla}\cdot\overrightarrow{D}) equal to 4\pi times the charge per volume, \rho, that made the lines of force in the first place.”

Now don’t worry about the 4\pi, he just added it to remove the 4\pi in the pressure equation. Like I said, Maxwell played around with 4\pi a lot and it just changes the value of a constant, so it does not really matter. What matters is that he just stated Gauss’s law without really spelling out how he got there, probably because it wasn’t clear to Maxwell… yet.

Despite how he “derived” it, these equations, [B] and [C] are just Gauss’s law. First, as I said before, in modern language equation [C] can be written as \overrightarrow{\nabla}\cdot\overrightarrow{D}=4\pi\rho.

Then, if you multiply both sides by k, and then use equation [B] that \overrightarrow{E}=k\overrightarrow{D}, you get that \overrightarrow{\nabla }\cdot\overrightarrow{E}=4\pi k \rho.

If you define a new constant, \epsilon, so that \epsilon=\frac{1}{4\pi k} , you get \overrightarrow{\nabla}\cdot\overrightarrow{E}=\rho/\epsilon which is Gauss’s law!

Maxwell was quite pleased with his results, and even the now frail and sickly 65-year-old Faraday loved it despite the math writing Maxwell, “[it] gives me much encouragement to think on. I was at first almost frightened when I saw such mathematical force made to bear upon the subject, and then wondered to see that the subject stood it so well.”^[34]

However, Maxwell needed an electric model of the atom rather than a wonky metaphor of imaginary fluids. Which brings me to…

Part 4: Maxwell’s “On Physical Lines of Force” (1861-62)

Maxwell with his new beard that he grew in 1856 to make himself look old enough to teach at a college.

In 1850, a Scottish scientist named William Rankine was inspired by Faraday to model the atom with what he called “molecular vortices.” This strangely named model is astonishingly modern as Rankine stated that, “each atom of matter consists of a nucleus, or a central physical point, enveloped by an elastic atmosphere, which is retained in its position by forces attracted towards the nucleus or center.”^[35]

After, Maxwell’s friend William Thomson started incorporating some of Rankine’s ideas into his papers and in 1861, Maxwell adjusted his view of electric and magnetic fields using this model of “molecular vortices” rather than the model of tubes of incompressible fluids in a series of papers titled “On Physical Lines of Force.”

These papers made some major changes to his laws, but in terms of Gauss’s law, this paper led to similar conclusions that he arrived with his “tubes of incompressible fluids,” paper with 2 important and multiple superficial differences.

The first important difference in Gauss’s law in this paper versus the last one was that in his first set of papers Maxwell just stated outright that the sum of derivatives was dependent on the charge density because it just made sense to him.

This time, Maxwell started with deriving another equation, specifically his equation that currently has the unwieldy name of, “Ampere Circuital Law with Maxwell’s addition.” Maxwell then used that equation to establish how the divergence of the electric field is related to the charge per volume (now given the letter lowercase “e”).

I will show in future videos how Maxwell did this and how Gauss’s law is just a mathematical consequence of Ampere’s law (and how Gauss’s law for magnetism is just a consequence of Maxwell’s “Faraday’s law”).

But for now, just put a pin in that statement and save it for later.

The second significant change in Gauss’s law in 1862 is that Maxwell gave a physical meaning to the “quantity of electric current” (that I called “quantity of electric lines”) from the sinks and sources.

If you remember when Maxwell first created the “quantity of electric current” he used an analogy to a current in a tube, where the electric field is analogous to the voltage and the “quantity of electric current” is how much these fields “flow” from sources to sinks, which depends on a “resistance.” These equations work, but they are basically physically meaningless.

In 1861 and 62, with the help of Rankine’s “molecular vortices” model, Maxwell could model how these lines of force interact with a dielectric saying, “in a dielectric under induction, we may conceive that the electricity in each molecule is so displaced that one side is rendered positively, and the other negatively electrical, but that the electricity… does not pass from one molecule to another.”^[36]

As the molecules in the dielectric are displaced, Maxwell renamed his “quantity of electric current” to be the “displacement,” a name it retains to this day.

Just as before, the “displacement” (or lines of force from a charge or set of charges) is related to the electric field by a constant. This time, however, the constant is not a “resistance” but instead a constant that is dependent “on the nature of the dielectric.”^[37]

As I said before, this didn’t change the nature of the equation at all, it only changed the meaning of the letters.

If you look at the equation as Maxwell wrote it in 1862, however, it looks very different than in 1855, but that has to do with the superficial changes that he made.

First, Maxwell added a 4\pito this relationship instead of to the Gauss’s law part, which makes no difference aside from changing the magnitude of the displacement field.

Second, he squared the constant, which he gave a new letter E. That sounds significant, but it only changes the value of the constant. Third, he made the displacement, (f,g,h), to be negative of the electric field, (P, Q, R). ^[38]

The reason he did this is because Maxwell decided he was interested in how the lines converge on the sources and sinks, instead of how the lines diverge away from them. For that reason, Maxwell made the displacement vector negative to the function we use currently (or he used the convergence of a negative displacement field -\overrightarrow{\nabla}\cdot\overrightarrow{D}' instead of the divergence of a positive displacement field \overrightarrow{\nabla}\cdot\overrightarrow{D}. ^[39]

This only changes the value of the displacement field but not the end result for force or electric potential.

(By the way, in 1883, Oliver Heaviside wrote about Gauss’s law and said that the “expression on the right side of this equation (with the – sign prefixed) Maxwell called the ‘convergence’ [but] we may as well use the term ‘divergence’ for the same quantity with a + sign prefixed.”^[40]

Back in 1862, Maxwell wrote Gauss’s law as one equation instead of two, so the charge per volume equals the divergence of the electric field times a constant. If use Maxwell’s old term \rho for e, use the Greek letter \epsilon for \frac{1}{4\pi E^2} and vector notation for the Electric Field, \overrightarrow{E} =(P,Q,R), Maxwell’s equation (115) transforms from:

e = \frac{1}{4\pi E^2}\bigg(\frac{dP}{dx}+\frac{dQ}{dy}+\frac{dR}{dz}\bigg)

To

\rho= \epsilon\overrightarrow{\nabla}\cdot\overrightarrow{E} \quad\quad \text{or} \quad\quad \overrightarrow{\nabla }\cdot\overrightarrow{E}=\frac{\rho}{\epsilon}

So, once again Gauss’s law, now with some physical meaning for the displacement way back in 1862.

However, there is one concept used in this equation that is still undeveloped: the constant \frac{1}{4\pi E^2} , was not given a name nor much of a physical meaning besides being related to the dielectric constant…somehow. That was all clarified in 1864 which brings us to… 

Part 5: Maxwell’s “Electric Elasticity” vs. Heaviside’s “Permittivity”

On December 8, 1864, 33-year-old James Clerk Maxwell wrote a paper where he used his new equations to describe how his laws could be used to mathematically explain light as a wave in an electromagnetic field (a phrase he coined for that very purpose).

[I know he looked much older, but I think that was to do with his big bushy beard which he grew to make him look more mature]

Anyway, this paper was to have major implications for the development of science, but in terms of Gauss’s law, it was very similar to before with 2 subtle changes, one superficial and one profound both about the relationship between the Electric Field represented by the letters (P, Q, R) and the Displacement field represented by the letters (f, g, h).

The superficial change is that Maxwell decided that if the Displacement is negative, the Electric field should be negative too, so this relation no longer has a negative sign. (Maxwell then changed the sign for the force and electric potential, so the results are the same.)

Second, and more interestingly, Maxwell decided to drop the 4\pi and the E^2 and go back to a simple constant k. So, the equation between the electric field and the displacement field:

P = kf \quad Q= kg \quad R=kh

is the exact same relationship as he found in 1856, namely:

\overrightarrow{E}=k \overrightarrow{D}

What makes this different is that in 1856, Maxwell did not give k a name besides a “resistance.”

In 1864, however, Maxwell called k the “electric elasticity” as he imagined the molecules in the dielectric being pulled by the electric displacement which then bounced back when the displacement field was removed. ^[41]

The more the dielectric was pulled by the displacement field, the smaller the “electric elasticity” is. Using this logic, the “elasticity” was inversely proportional to the dielectric constant.

Finally, we have Gauss’s law where every letter has a physical meaning.

It was Oliver Heaviside who, in the 1880s and early 1890s, decided that it was often more logical to define the constant (which he called the permittivity) if you defined it as the ratio of D/E rather than E/D so that it is linearly proportional to the dielectric constant. In other words, define a new constant, the permittivity, that Heaviside labeled “c” but we currently use the Greek letter epsilon, \epsilon, that is one over the elasticity, where \epsilon=1/k. That way, instead of \overrightarrow{E} =k \overrightarrow{D}, you get:

\overrightarrow{E} = \frac{\overrightarrow{D}}{\epsilon}

The advantages of using the Heaviside’s permittivity over Maxwell’s electric elasticity is that you can see visually that the electric field is reduced by the value of the dielectric constant.

Note that even if the field was going through a vacuum, which has no molecules to be pulled by the displacement field, or air at room temperature or pressure, which reduces the value by a factor of 1.0006, you still often need a constant to make the units work out.

This constant is currently called the permittivity of free space or \epsilon_0 (pronounced epsilon zero or epsilon naught – naught as in an old-fashioned way of saying nothing, as in “naught but a fool”) and is so common a situation that we are often taught Gauss’s equation for that case.

Which is exactly what Richard Feynman wrote as Gauss’s law in 1962. Roll the tape!

So that is the historical origin of Gauss’s law.

But how and why did we get from Maxwell’s version of Gauss’s law in 1864 to the “modern” version taught by Feynmen almost a hundred years later in 1962?

What does that have to do with math functions called quaternions?

Why did Oliver Heaviside get involved and what about the influences of William Hamilton, Peter Tait, Josiah Williard Gibbs and even Heinrich Hertz?

If you haven’t subscribed or hit the bell yet you really should because the answer to all of that and more is next time on the lightning tamers!

Whew, that was a pretty hardcore physics video for me: I usually give a lot more space to tell the personal stories of the scientists and give some mental space and context between physics ideas, but I felt like this story needed to be told, even if it was intense.

Also, you can learn about my new book “The Lightning Tamers” about the history of electricity and how it ended up powering our world.

Heck, you can even download over 100 pages of “The Lightning Tamers” for free.

It is available for pre-order on Amazon and from your favorite bookstore – I am also hosting a go fund me for making an audiobook and you can get information about all that and more on my website.

Thank you to my Patrons, and remember to stay safe and curious, my friends. Bye.^[42]

---

References:

^[1] Phillips, Rob “In Retrospect: The Feynman Lectures on Physics” Nature vol. 504 (2013), p. 30 https://www.nature.com/articles/504030a

^[2] Feynman, R The Feynman Lectures on Physics vol. 2, (1964) p. 1-11 https://www.feynmanlectures.caltech.edu/II_01.html#Ch1-S1

^[3] Feynman, R The Feynman Lectures on Physics vol. 2, (1964) p. 18-2 https://www.feynmanlectures.caltech.edu/II_18.html

^[4] Feynman Lectures [#S2 5:15-5:55] https://www.feynmanlectures.caltech.edu/flptapes.html

^[5] Keithley, Joseph The Story of Electrical and Magnetic Measurements (1999), p. 43 https://www.google.com/books/edition/The_Story_of_Electrical_and_Magnetic_Mea/uwgNAtqSHuQC?hl=en&gbpv=0

^[6] According to Munro, J Pioneers of Electricity (1890) p. 81 https://www.google.com/books/edition/Pioneers_of_Electricity_Or_Short_Lives_o/SAgJAAAAIAAJ?hl=en&gbpv=0

^[7] Coulomb, C “Law of Electric Force and the Fundamental Law of Electricity” translated and found in Kuehn, K A Student’s Guide Through the Great Physics Texts Vol III (2015) p. 71 https://www.google.com/books/edition/A_Student_s_Guide_Through_the_Great_Phys/Ayo3CwAAQBAJ?hl=en&gbpv=0

^[8] Coulomb, C “Second Memoire” p. 611 Mémoires sur l’électricité et la magnétisme : Coulomb, C. A. (Charles Augustin), 1736-1806 : Free Download, Borrow, and Streaming : Internet Archive

^[9] Coulomb “A Fourth Memoir on Electricity, in which two principal Properties of the Electric Fluid are Demonstrated” The Monthy review, or, literary journal vol. 81 (1789), 604 In French (p. 69):.Mémoires sur l’électricité et la magnétisme : Coulomb, C. A. (Charles Augustin), 1736-1806 : Free Download, Borrow, and Streaming : Internet Archive https://www.google.com/books/edition/The_monthly_review_or_literary_journal/X5tKAAAAcAAJ?hl=en&gbpv=1&dq=“A+Fourth+Memoir+on+Electricity,+in+which+two+principal+Properties+of+the+Electric+Fluid+are+Demonstrated”&pg=PA604&printsec=frontcover

^[10] Michael Faraday, “Experimental Researches in Electricity – Series 11” (Dec 21, 1837) Proceedings of the Royal Society vol 128 (1838), p. 5 https://doi.org/10.1098/rstl.1838.0002

^[11]Michael Faraday, “Experimental Researches in Electricity – Series 11” (Dec 21, 1837) Proceedings of the Royal Society vol 128 (1838), p. 20 https://doi.org/10.1098/rstl.1838.0002

^[12] Michael Faraday, “Experimental Researches in Electricity – Series 11” (Dec 21, 1837) Proceedings of the Royal Society vol 128 (1838), p. 20 https://doi.org/10.1098/rstl.1838.0002

^[13] Faraday, M (Nov, 1845) “19^th Series” Experimental Researches in Electricity: Vol 3 (1855) p. 2 https://www.google.com/books/edition/_/9m-FAAAAIAAJ?gbpv=0

^[14] Faraday, “Experimental Researches in Electricity – Series 11” (Dec 21, 1837) Proceedings of the Royal Society vol 128 (1838), p. 2 https://doi.org/10.1098/rstl.1838.0002

^[15] Faraday, “Experimental Researches in Electricity – Series 11” (Dec 21, 1837) Proceedings of the Royal Society vol 128 (1838), p. 25 https://doi.org/10.1098/rstl.1838.0002

^[16] Faraday, “Experimental Researches in Electricity – Series 11” (Dec 21, 1837) Proceedings of the Royal Society vol 128 (1838), p. 31 https://doi.org/10.1098/rstl.1838.0002

^[17] Michael Faraday “Experimental Researches in Electricity – Series 12, 13, and 14” (January, February and June 1838) https://doi.org/10.1098/rstl.1838.0008, https://doi.org/10.1098/rstl.1838.0009, https://doi.org/10.1098/rstl.1838.0014

^[18] Hirshfeld, Alan The Electric Life of Michael Faraday (2009) p. 149 (<- fabulous book by the way) https://www.google.com/books/edition/The_Electric_Life_of_Michael_Faraday/OJS7uOC2XCoC?hl=en&gbpv=0

^[19] Dr. Latham to Bande (Dec 1, 1839) Thompson, Silvanus Michael Faraday: His Life and Work (1898) p. 222 https://www.google.com/books/edition/Michael_Faraday/Yj0DAAAAYAAJ?hl=en&gbpv=0

^[20] Faraday, “ERE – 19” (Nov, 1845) Proceedings of the Royal Society vol 136 (1856) p. 1 I. Experimental researches in electricity.—Nineteenth series (royalsocietypublishing.org)

^[21] Faraday “Thoughts on Ray-vibrations” (May, 1846) The London, Edinburgh and Dublin Phil Magazine vol. 28 p. 345 ser.3:v.28 (1846:Jan.-June) – The London, Edinburgh and Dublin philosophical magazine and journal of science – Biodiversity Heritage Library (biodiversitylibrary.org)

^[22] Maxwell to Thomson (Feb 20, 1854) found in The Life of William Thomson , vol 1 (1910) p. 304 The Life of William Thomson, Baron Kelvin of Largs – Google Books

^[23] Maxwell, J. Clerk A Treatise on Electricity and Magnetism Vol 1, p. ix-x https://www.google.com/books/edition/A_Treatise_on_Electricity_and_Magnetism/gokfAQAAMAAJ?hl=en&gbpv=0

^[24] Maxwell, James Clerk “On Faraday’s Lines of Force” (read Dec 1855, Feb 1856) The Scientific Papers of James Clerk Maxwell vol. 1 (1890) p. 157-8 https://www.google.com/books/edition/The_Scientific_Papers_of_James_Clerk_Max/edlCAQAAMAAJ?hl=en&gbpv=0

^[25] Lewis Cambell and William Garnett, The Life of James Clerk Maxwell (1882) p. 517 https://www.google.com/books/edition/The_Life_of_James_Clerk_Maxwell/a_xAAQAAIAAJ?hl=en&gbpv=1&dq=The+Life+of+James+Clerk+Maxwell+(1882)&printsec=frontcover

^[26] Maxwell, James Clerk “On Faraday’s Lines of Force” (read Dec 1855, Feb 1856) The Scientific Papers of James Clerk Maxwell vol. 1 (1890) p. 158 https://www.google.com/books/edition/The_Scientific_Papers_of_James_Clerk_Max/edlCAQAAMAAJ?hl=en&gbpv=0

^[27] Maxwell, James Clerk “On Faraday’s Lines of Force” (read Dec 1855, Feb 1856) The Scientific Papers of James Clerk Maxwell vol. 1 (1890) p. 160 https://www.google.com/books/edition/The_Scientific_Papers_of_James_Clerk_Max/edlCAQAAMAAJ?hl=en&gbpv=0

^[28] Maxwell, James Clerk “On Faraday’s Lines of Force” (read Dec 1855, Feb 1856) The Scientific Papers of James Clerk Maxwell vol. 1 (1890) p. 162 https://www.google.com/books/edition/The_Scientific_Papers_of_James_Clerk_Max/edlCAQAAMAAJ?hl=en&gbpv=0

^[29] Maxwell, James Clerk “On Faraday’s Lines of Force” (read Dec 1855, Feb 1856) The Scientific Papers of James Clerk Maxwell vol. 1 (1890) p. 164 https://www.google.com/books/edition/The_Scientific_Papers_of_James_Clerk_Max/edlCAQAAMAAJ?hl=en&gbpv=0

^[30] Maxwell, James Clerk “On Faraday’s Lines of Force” (read Dec 1855, Feb 1856) The Scientific Papers of James Clerk Maxwell vol. 1 (1890) p. 180-1 https://www.google.com/books/edition/The_Scientific_Papers_of_James_Clerk_Max/edlCAQAAMAAJ?hl=en&gbpv=0

^[31] Maxwell, James Clerk “On Faraday’s Lines of Force” (read Dec 1855, Feb 1856) The Scientific Papers of James Clerk Maxwell vol. 1 (1890) p. 174 https://www.google.com/books/edition/The_Scientific_Papers_of_James_Clerk_Max/edlCAQAAMAAJ?hl=en&gbpv=0

^[32] Maxwell, James Clerk “On Faraday’s Lines of Force” (read Dec 1855, Feb 1856) The Scientific Papers of James Clerk Maxwell vol. 1 (1890) p. 191 https://www.google.com/books/edition/The_Scientific_Papers_of_James_Clerk_Max/edlCAQAAMAAJ?hl=en&gbpv=0

^[33]  Maxwell, James Clerk “On Faraday’s Lines of Force” (read Dec 1855, Feb 1856) The Scientific Papers of James Clerk Maxwell vol. 1 (1890) p. 191 https://www.google.com/books/edition/The_Scientific_Papers_of_James_Clerk_Max/edlCAQAAMAAJ?hl=en&gbpv=0

^[34] Faraday to Maxwell quoted in “Memorial to James Clerk Maxwell” The London Quarterly Review vol. 60 (1883) p. 24 https://www.google.com/books/edition/The_London_Quarterly_Review/bn84AQAAMAAJ?hl=en&gbpv=1

^[35] Rankine, William “On the Mechanical Action of Heat” (Feb 4, 1850) Trans of the Royal Society of Edinburgh vol. xx p. 147 https://www.biodiversitylibrary.org/item/126047#page/177/mode/1up

^[36] Maxwell “On Physical Lines of Force: Part III” (read Jan, Feb, 1862) The Scientific Papers of James Clerk Maxwell vol. 1 (1890) p. 491 https://www.google.com/books/edition/The_Scientific_Papers_of_James_Clerk_Max/edlCAQAAMAAJ?hl=en&gbpv=0

^[37] Maxwell “On Physical Lines of Force: Part III” (read Jan, Feb, 1862) The Scientific Papers of James Clerk Maxwell vol. 1 (1890) p. 491 https://www.google.com/books/edition/The_Scientific_Papers_of_James_Clerk_Max/edlCAQAAMAAJ?hl=en&gbpv=0

^[38] Maxwell “On Physical Lines of Force: Part III” (read Jan, Feb, 1862) The Scientific Papers of James Clerk Maxwell vol. 1 (1890) p. 497 https://www.google.com/books/edition/The_Scientific_Papers_of_James_Clerk_Max/edlCAQAAMAAJ?hl=en&gbpv=0

^[39]  In 1883, Oliver Heaviside switched it back writing,  “we may as well use the term ‘divergance’ for the same quantity with the + sign prefixed [so that] if the amount of divergence be positive, it indicates positive electricity.” Heaviside, Oliver “Some Electrostatic & Magnetic Relations” (April 14, 1883) The Electrician vol. 10 p. 510

https://www.google.com/books/edition/The_Electrician/uRhbAAAAYAAJ?hl=en&gbpv=1&bsq=Heaviside%20

^[40]  Heaviside, Oliver “Some Electrostatic & Magnetic Relations” (April 14, 1883) The Electrician vol. 10 p. 510 https://www.google.com/books/edition/The_Electrician/uRhbAAAAYAAJ?hl=en&gbpv=1&bsq=Heaviside%20

^[41] Maxwell “A Dynamical Theory of the Electromagnetic Field” (Read Nov, 1864) The Scientific Papers of James Clerk Maxwell vol. 1 (1890) p. 560 https://www.google.com/books/edition/The_Scientific_Papers_of_James_Clerk_Max/edlCAQAAMAAJ?hl=en&gbpv=0

^[42] Heaviside started talking about this in 1884, named the permittivity in 1887, but his recap written in 1891 is the most clear IMHO: Heaviside (Feb 13, 1891) “Electric and Magnetic Force” found in Electrical Papers Vol. 1 (1892) p. 21 https://www.google.com/books/edition/Electromagnetic_Theory/_Zk3AAAAMAAJ?hl=en&gbpv=0
(I will go into this more in my next video)